To simulate axis switching transitions, add an
"Axis Switching" object under a transition moment object;
currently it is implemented for Cartesian or Spherical
transition moments for asymmetric tops. The rotation between the
axes in the two states is specified by the three Euler angles:
The basic theory was originally described in
Hougen and Watson (1964). The implementation here is more general,
using an exact evaluations of the Wigner D matrix and not assuming
that
K is a good quantum number, rather than the
approximations used by Hougen and Watson. It is also implemented
for multiphoton transitions. More general results can be found in
Dixon and Wright (1985) (for rotation about a single axis, θ) and
Huet at al (1990) (including all thee axes). The formula used
relies on the fact that the wavefunctions have the form of Wigner
D matrices (Brown and Howard, 1976):
|NMK> = [(2J+1)/(8π2)]½DMK
N(ω)*
and rotating the the Wigner D matrices though the axis switching
angles (χ
T, θ
T, φ
T) produces a
sum over Wigner D matrices with the same
N and
M:
DMK N(ω')
= ΣK' DK'K N(χT,
θT, φT) DMK' N(ω)
Now consider an arbitrary transition dipole moment, <
N'M'K';
ω'|
T | NMK;
ω>, where the body
fixed axes in the bra and ket are different and ω' represents the
angle between the space and body fixed angles used for the bra and
ω for the ket. Using the equation above we can transform the bra
the bra to use the axis system of the ket:
<N'M'K'; ω'| = [(2J+1)/(8π2)]½DM'K'
N'(ω') = [(2J+1)/(8π2)]½
ΣK" DK"K' N'(χT,
θT, φT) DM'K" N'(ω)
= ΣK" DK"K' N'(χT,
θT, φT) <N'M'K"; ω|
The transition moment can thus be expressed in terms of rotational
matrix elements all in the same axis system:
<N'M'K'; ω'| T |NMK;
ω> = ΣK" DK"K' N'(χT,
θT, φT)<N'M'K"; ω| T
|NMK; ω>
and the transition dipole matrix elements <
N'M'K";
ω|
T | NMK;
ω> are now the standard ones
used by
PGOPHER.
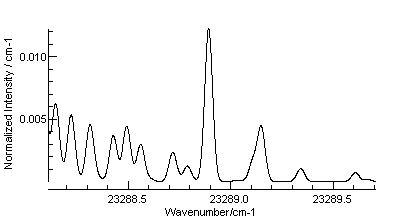
Example - HSiF
The datafile HSiFswitching.pgo
produces the simulation shown below, which reproduces the right
hand 2/3 of figure 3c of Dixon and Wright (1985). Note the axis
switching angle, θT, set to 2.3 in the "Axis Switch"
object under the T(1,1) Spherical
transition moment. To reproduce figure 3b, with no axis
switching, set the angle to 0. Note the choice of axes is
important - θT is the rotation about an axis
perpendicular to the axis defining K.