| |
<Prev Next> |
| Nucleus | Index, starting from 1, of the nuclear spin involved in perturbation; 0 (the default) for those not involving a nuclear spin. |
| SymSelect | Possible values are all
(normal use), e_only
(only affect e
levels) and f_only
(only affect f
levels). Was ParitySelect in previous versions. |
| ScalePrev | Scale factor with respect to preceding perturbation |
| Op | Perturbation type. See below for possible values. If only
Npower and/or Srank, Scomp are
needed, use Op = Luncouple with n = 0. |
| n | Power of operator in perturbation. |
| Npower | Power of N (for centrifugal distortion of
perturbation). Perturbation operator is ½[N2,Op]+.
If RSquaredH
is set, N is replaced by R. |
| OmegaSelect | Set to all (the default) for normal use; set to a specific value to restrict the perturbation to a specific value of Ω. Note that the current implementation applies the constraint to both connected wavefunctions, so is only useful for ΔΩ = 0 matrix elements. |
| Srank | If Srank <= 0: adds a
term S±Scomp and changes the
power of J or N. See the Op
details below. If Srank > 0: spherical tensor operator for S with overall rank Srank and component Scomp. Note that both of these are only implemented for Op = Luncouple, Suncouple and LNuncouple. Versions before 10.033 require Srank < 0 for S±Scomp. |
| Scomp |
| Value | Size of perturbation; the expressions and operators given
below should be understood to be multiplied by this. |
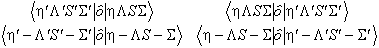
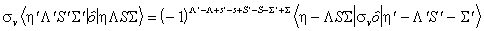
| Name |
Operator |
Op |
n |
Npower |
Srank |
Scomp |
Scale Factor |
Notes |
| B | N2 |
(Luncouple) | 0 | 2 | 0 | 0 | 1 | N2 is replaced by R2 if RSquaredH is set |
| D | N4 | (Luncouple) | 0 | 4 | 0 | 0 | -1 | N4 is replaced by R4 if RSquaredH is set |
| H | N6 | (Luncouple) | 0 | 6 | 0 | 0 | 1 | N6 is replaced by R6 if RSquaredH is set |
| L | N8 | (Luncouple) | 0 | 8 | 0 | 0 | 1 | N8 is replaced by R8 if RSquaredH is set |
| M | N10 | (Luncouple) | 0 | 10 | 0 | 0 | 1 | N10 is replaced by R10 if RSquaredH is set |
| PP | N12 | (Luncouple) | 0 | 12 | 0 | 0 | 1 | N12 is replaced by R12 if RSquaredH is set |
| A | see above |
LS | 1 | 0 | 0 | 0 | 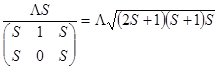 which gives the LzSz operator form |
|
| AD | see above |
LS | 1 | 2 | 0 | 0 | Scale factor as for A above which gives the ½[N2,LzSz]+ operator form | |
| AH | see above |
LS | 1 | 4 |
0 | 0 | Scale factor as for A above which gives the ½[N4,LzSz]+ operator form | |
| AL | see above |
LS | 1 | 6 |
0 | 0 | Scale factor as for A above which gives the ½[N6,LzSz]+ operator form | |
| AM | see above |
LS | 1 | 8 |
0 | 0 | Scale factor as for A above which gives the ½[N8,LzSz]+ operator form | |
| gamma | N.S |
NS | 1 | 0 | 0 | 0 | 1 | |
| gammaD | ½[N2,N.S]+ | NS | 1 | 2 | 0 | 0 | 1 | N2 (only) is replaced by R2 if RSquaredH is set |
| gammaH | ½[N4,N.S]+ | NS | 1 | 4 | 0 | 0 | 1 | N4 (only) is replaced by R4 if RSquaredH is set |
| gammaL | ½[N6,N.S]+ | NS | 1 | 6 | 0 | 0 | 1 | N6 (only) is replaced by R6 if RSquaredH is set |
| LambdaSS | 6-½(3Sz2-S2) | (Luncouple) | 0 | 0 | 2 |
0 | (8/3)½ | |
| LambdaD | ½[N2,6-½(3Sz2-S2)]+ | (Luncouple) | 0 | 2 | 2 |
0 | (8/3)½ | N2 (only) is replaced by R2 if RSquaredH is set |
| LambdaH | ½[N4,6-½(3Sz2-S2)]+ | (Luncouple) | 0 | 4 | 2 |
0 | (8/3)½ | N4 (only) is replaced by R4 if RSquaredH is set |
| theta | 280-½(35Sz4-20S2Sz2+25Sz2-6S2+3S4) | (Luncouple) | 0 | 0 | 4 |
0 | (35/18)½ | |
For all of these operators, the N is replaced by R
if RSquaredH
is set; the N+ and N-
operators are not changed.
| Name |
Operator |
Op |
n |
Npower |
Srank |
Scomp |
Scale Factor |
| o | S+2L-2+S-2L+2 | LNuncouple | 2 | 0 | -1 | -2 | ½ |
| oD | ½[N2,S+2L-2+S-2L+2]+ | LNuncouple | 2 | 2 | -1 | -2 | ½ |
| oH | ½[N4,S+2L-2+S-2L+2]+ | LNuncouple | 2 | 4 | -1 | -2 | ½ |
| oL | ½[N6,S+2L-2+S-2L+2]+ | LNuncouple | 2 | 6 | -1 | -2 | ½ |
| p | N+S+L-2+N-S-L+2 | LNuncouple | 2 | 0 | -1 | -1 | -½ |
| pD | ½[N2,N+S+L-2+N-S-L+2]+ | LNuncouple | 2 | 2 | -1 | -1 | -½ |
| pH | ½[N4,N+S+L-2+N-S-L+2]+ | LNuncouple | 2 | 4 | -1 | -1 | -½ |
| pL | ½[N6,N+S+L-2+N-S-L+2]+ | LNuncouple | 2 | 6 | -1 | -1 | -½ |
| q | N+2L-2+N-2L+2 | LNuncouple | 2 | 0 | 0 | 0 | ½ |
| qD | ½[N2,N+2L-2+N-2L+2]+ | LNuncouple | 2 | 2 | 0 | 0 | ½ |
| qH | ½[N4,N+2L-2+N-2L+2]+ | LNuncouple | 2 | 4 | 0 | 0 | ½ |
| qL | ½[N6,N+2L-2+N-2L+2]+ | LNuncouple | 2 | 6 | 0 | 0 | ½ |
A few lambda doubling operators for Δ
states are built into PGOPHER, though note that these
use the form involving J rather than N, and the
name is not standard for some of them. The form involving N
can be obtained by replacing Luncouple with LNuncouple
and lambda operators for higher values of Λ can be obtained
by setting n = 2Λ. Centrifugal distortion can be
added using NPower, as for Π states above.
| Name |
Operator |
Op |
n |
NPower |
Srank |
Scomp |
Scale Factor |
Notes |
| o | S+4L-4+S-4L+4 | Luncouple | 4 | 0 | -1 | -4 | ½ | The conventional name would be m |
| oD | J+S+3L-4+J-S-3L+4 | Luncouple | 4 | 0 | -1 | -3 | -½ | The conventional name would be n |
| oH | J+2S+2L-4+J-2S-2L+4 | Luncouple | 4 | 0 | -1 | -2 | ½ | The conventional name would be o |
| p | J+3S+L-4+J-3S-L+4 | Luncouple | 4 | 0 | -1 | -1 | -½ | |
| q | J+4L-4+J-4L+4 | Luncouple | 4 | 0 | 0 | 0 | ½ |