| |
<Prev Next> |
The force field can be expressed in terms of valence or
symmetry coordinates. A typical analysis will include several
isotopologues and might have a data file structured something
like this:
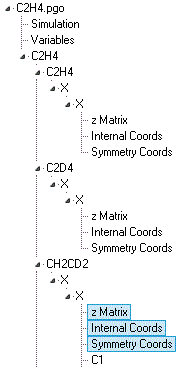
Note the various single and multiple objects:
A Cartesian Coordinates
object may also be present; the exact combination of objects
used depends on the required calculation. Nuclear Co-ordinates and Vibrational Modes objects will
also be present, automatically created and updated from the
force field analysis objects listed above.
The current version of the program does not explicitly make use of symmetry for the force field analysis, but it is implicit in the way the force constants and geometry are specified. The current version of PGOPHER is restricted to harmonic terms, but the program is structured so that anhamonic terms can be added in future. The units are currently less flexible than for rotational calculations; the overall mixture units must be set to cm-1, the geometry specified in Angstroms and degrees and force constants (for stretches) in millidyne/Å = aJ/Å2 (1 millidyne/Å = 1 aJ/Å2 = 100 J/m2 = 100 N/m). For a full discussion of the units see Hedberg and Mills (1993).
The 3N-6 (or more) internal coordinates, R, are defined in terms of a matrix, B, that transforms between the 3N Cartesian displacements, Δx and R:
R = B Δx
B can be specified directly with a Cartesian Coordinates object, or
in terms of Valence Coordinates
with an Internal Coordinates
object. The potential energy can be specified in terms of internal
co-ordinates:
V = ½ RT f RThe implementation permits redundant internal coordinates (i.e. more than 3N-6), but some constraints on the force field will be required in these circumstances as a force field specified in terms of redundant coordinates is not unique.
ρ = M½Δx = l Qwhere M is a 3N×3N matrix with the nuclear masses on the diagonal. The related adm matrix is also used in some contexts, defined by adm = M-½ l so that:
Δx = M-½ l Q = adm QWith this definition of l and Q the kinetic energy is diagonal, provided the l matrix is orthogonal:
2T = ρ' ρ' = Q'T lT l Q' = Q'T Q' = Σi Qi'2where ' is used to indicate d/dt (classically) or Pi = -ih/2π d/dQi (quantum mechanically). To understand the method used to work out the l matrix, consider the potential energy expressed in mass weighted Cartesian coordinates using the equations for R, V and ρ above:
2V = ρT M-½ BT f B M-½ρThis can be rewritten in terms of normal coordinates using ρ = l Q:
2V = QT lT M-½ BT f B M-½ l Q = QT lT GF l Qwhere the GF matrix has been defined (in a non-standard way) as:
GF = M-½ BT f B M-½The l matrix is then computed to be the eigenvectors of the GF matrix so that:
lT GF l = λ
2V = QT λ Q = Σi λi Qi2
qi = γi1/2 QiIf the scaling factor is chosen to be γi = 2πλi1/2/h the total energy has a particularly simple form:
T + V = ½ Σi (Pi2 + λi Qi2) = ½ Σi (2π)-1 h λi½ (pi2 + qi2) = ½ Σi hνi(pi2 + qi2)
which also makes qi dimensionless as required and identifies λi½ as 2πνi. The transformation matrix between these dimensionless normal coordinates and Cartesian displacements, which we define as d, is then given by:
Δx = M-½ l Q = M-½ l γ-½ q = d qFor a harmonic oscillator this the range of the zero point motion is ±1, so the elements of this matrix give the range of the zero point motion. The transformation matrix between dimensionless normal coordinates and internal coordinates, dint, follows from this:
R = B Δx = B M-½ l γ-½ q = B d q = dint q
S = U R = U B Δx
V = ½ ST F S
f = UT F U
G = U B M-1BT UTand Choleski decomposition is used to factorise the G matrix such that:
G = C CTwhere C is a lower triangular matrix. The matrix CT F C has the same eigenvalues, λ, as the GF matrix, and the eigenvectors, V, can be used to calculate the transformation matrix, L, between the symmetry and normal coordinates:
S = C V Q = L Qand the transformation matrix, dsym, between the symmetry and dimensionless normal coordinates:
S = L Q = L γ-½ q = dsym qGiven L the following can be calculated:
(L-1)T = F L λ-1where A is the matrix that transforms symmetry coordinates to Cartesian coordinates:
G-1 = (L-1)T L-1
A = M-1BTG-1 = M-1BT(L-1)T L-1
Δx = A SIn practice the matrix A L = M-1BT(L-1)T is calculated as the l matrix can be calculated from:
l = M½ A L