| <Prev Next> |
Given the line strengths S or Spol discussed in Transition Moments and Line Strengths, the IntensityUnits setting then controls how the spectrum is plotted. The simplest is HonlLondon, which simply plots the line strength calculated as 3Spol, ignoring population effects. (For simple allowed branches, the result is typically approximately proportional to J; see Transition Moments and Line Strengths for why 3Spol is chosen here.)
For spontaneous emission we have the Einstein A coefficient:
![]()
giving the rate of spontaneous emission from state A to state B as proportional to ν3S. Introducing the conversion factor to Debye (c–110–21) for the transition moments the fundamental constants combine to give a conversion factor of
![]()
= 1.163965505×10-20 s-1MHz-3Debye-2 for νAB in MHz and using the CODATA 2010 values. (Note that versions before 8.0.189 used CODATA 2006 values, and versions after 9.0 use CODATA 2014 values.) For νAB in cm–1 the conversion factor becomes
![]() =3.13618894×10-7 s-1cm-3Debye-2
=3.13618894×10-7 s-1cm-3Debye-2
The treatment of the sum over
degenerate (M) states requires some consideration. To
obtain the total emission intensity on a particular transition,
the sum over both the upper and lower degenerate states should be
taken. This occurs when S is used for ![]() ,
and is used in PGOPHER
when IntensityUnits
= EinsteinASum:
,
and is used in PGOPHER
when IntensityUnits
= EinsteinASum:
EinsteinASum / s-1 = 3.13618894×10-7 ν3/cm-3 S/ Debye2
If the radiative rate of the upper state is required then only the sum over lower states is needed, so the line strength divided by the upper state degeneracy should be used. (The intensity must be independent of the upper state M quantum number by virtue of the symmetry of free space.) For this set IntensityUnits = EinsteinA:
EinsteinA
/ s-1 = 3.13618894×10-7 ν3/cm-3
S/ Debye2 1/gupper
Note that the later behaviour was introduced after version 6.0.228; previous versions did not have EinsteinASum and IntensityUnits = EinsteinA gave the current EinsteinASum behaviour.
To model a real spectrum, level populations must be included, normally calculated using the Boltzmann equation. The raw lower state population can be plotted with IntensityUnits = PopDist, which plots an energy level diagram for the lower state, rather than a spectrum, with the intensity the Boltzmann factor:
![]()
IntensityUnits = NormPopDist divides this value by the partition function, Q:
![]()
defined so the populations add up to 1. When evaluating this sum, pgopher includes all manifolds with Initial set to true. NormPopDist then plots the fraction of molecules in any given level:
![]()
The simplest and quickest form that approaches a real spectrum is with IntensityUnits = Arbitrary. This is simply the line strength times the Boltzmann factor:
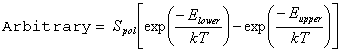
The Boltzmann factor for both the upper and the lower state is shown here, though the factor is only included for a particular state if the Initial flag is set for the Manifold. Note the use of Spol rather than S (to ensure multiphoton transitions are correct) and that the degeneracy factor is included in Spol.
The Saturation parameter can be used to adjust this, and the other calculations below using S or Spol to account for the effects of saturation. S is replaced by
![]()
where g = Min(2J'+1, 2J"+1) × Statistical Weight. This is appropriate for saturation by z polarized light. Increasing the Saturation parameter from zero makes the transition dipole moment progressively less important. Values of 1 to 10 will wash out the differences between allowed branches and much higher values will bring out transitions that are only allowed by some weak mixing.
IntensityUnits = Squared simply squares this value
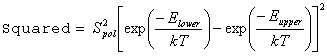
This mode gives a reasonable first approximation to intensities for degenerate four wave mixing spectroscopy.
While IntensityUnits = Arbitrary will give correct relative intensities for a single isotopic species, use of this form can give misleading results when simulating isotopologues or isotopomers with different symmetry or statistical weights, such as 35Cl2 and 35Cl37Cl. This is because the partition function is essential for the statistical weight calculation.
The accurate form is IntensityUnits = Normalized, which includes the partition function:
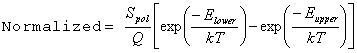
This is the recommended form for all types of spectroscopy unless absolute intensities are required; the more specific cases below are all only appropriate for one photon transitions.
For absolute intensities the starting point is the equation for the integrated absorption coefficient, ε, in terms of dipole moment for a molecule in a single state:
![]()
which gives the absorption coefficient as having units of molecule–1m2s–1. This is appropriate for a molecule in a single quantum state and ignores stimulated emission. To allow for a spread of states the Boltzmann factor must be added, and taking the sum over degenerate levels gives:
![]()
Introducing the line strength gives the final form:
![]()
Note that the degeneracies do not appear in this formula as they are included, by definition, in S and Q. Using Debye as the unit of dipole moment introduces a conversion factor of c–110–21. Converting the area to nm2 gives the constant as:
![]() = 4.16237933×10-5 nm2/Debye2
= 4.16237933×10-5 nm2/Debye2
using:
![]()
For νAB in MHz this gives the absorption intensity in nm2 MHz molecule–1, giving the final equation for IntensityUnits = nm2MHzperMolecule:
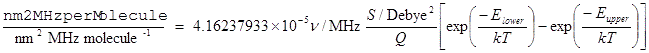
Note S is used rather than Spol, as it only applies to one photon transitions.
Alternatively, for νAB in cm–1 this would give units of nm2 cm–1 molecule–1, which can be converted to the more normal cm2 cm–1 molecule–1 = cm molecule–1 by multiplying by 10–14 giving an overall factor of:
4.16237933×10-19 nm2/Debye2
(Note that the conversion factor between nm2 MHz molecule–1 and cm molecule–1 involves an extra factor of 10–4 c to allow for the frequency conversion.)
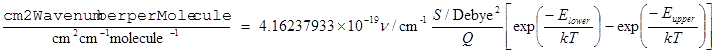
For emission spectra the appropriate scaling is as for the Einstein A coefficient, with a ν3 scaling factor. IntensityUnits = HzperMolecule thus adds the population factors to EinsteinASum:
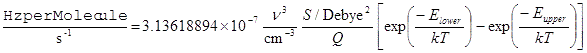
For this to be physically meaningful Initial should be set to true in the upper manifold of the transition, and the Fluorescence and AbsoluteE flags also set true in which case the Boltzmann factor is simply exp(-Eupper/kT). See Emission Spectra for further discussion of this. IntensityUnits = WperMolecule is also available, which scales the above by hν giving units of W/molecule.
For magnetic dipole transitions, the above equations can be used, provided the quantity:
![]()
is replaced by
![]()
where ![]() M
is now the magnetic dipole operator. The electric dipole
equivalent to a magnetic dipole can be found by equating these
two, giving:
M
is now the magnetic dipole operator. The electric dipole
equivalent to a magnetic dipole can be found by equating these
two, giving:
![]()
Converting the magnetic moment to units of the Bohr magneton, and the electric dipole moment to Debye gives an overall conversion factor of
![]() = 0.00927401 Debye/Bohr Magneton
= 0.00927401 Debye/Bohr Magneton
with an extra scaling factor of me/mp for nuclear magnetons. These scaling factors are included when evaluating matrix elements of magnetic moments of spins.
Overlays also have intensity units, though the interpretation is not exactly the same as above. Conversion to the same intensity units as set in the simulation object are done before plotting where the conversion makes sense, though some (such as between EinsteinASum and EinsteinA) are impossible because the information is not available. There is also an additional distinction between Arbitrary and Normalized – for the former the overlaid spectrum will always be scaled to fill the full range available, whereas with Normalized the relative scales of separate spectra will be preserved.