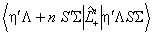LS
|
|
Spin orbit coupling, with the Ω
dependence from the Wigner-Eckart theorem; see for example
Lefebvre-Brion and
Field, 2nd Edition Equation 3.4.36:
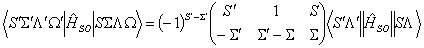
The perturbation parameter is the reduced matrix element  arranged so that Λ' > Λ and Λ' > 0
(or S' > S if Λ' = Λ). It is perhaps more
normal to quote the value including the 3j
symbol, but this is ambiguous when the spin-orbit operator connects
more than one component of a pair of states. Some common non-zero
values of the 3j symbol are
tabulated below. arranged so that Λ' > Λ and Λ' > 0
(or S' > S if Λ' = Λ). It is perhaps more
normal to quote the value including the 3j
symbol, but this is ambiguous when the spin-orbit operator connects
more than one component of a pair of states. Some common non-zero
values of the 3j symbol are
tabulated below.
| S. |
Σ' |
S |
Σ |
 |
| ½ |
-½ |
½ |
½ |
 |
| ½ |
½ |
½ |
½ |

|
| 1 |
0 |
0 |
0 |

|
| 1 |
1 |
0 |
0 |

|
| 1 |
1 |
1 |
1 |

|
| 1 |
1 |
1 |
0 |

|
|
Luncouple
|
J+nL-n+J-nL+n
|
L uncoupling; Using the default
n = 1 this can be used to model the  term omitted from the rotational operator. The perturbation parameter
is the value of the matrix element:
term omitted from the rotational operator. The perturbation parameter
is the value of the matrix element:
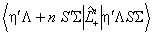
for Λ > 0 with the matrix element of L- derived by symmetry. |
Suncouple
|
J+nS-n+J-nS+n |
S uncoupling. (Note that this
term with n = 1 is present in the normal
Hamiltonian within a single vibronic state; it only makes sense to add
it as a
perturbation between states.) It checks for ΔΛ = 0 and |ΔΣ| = n,
but does not check for ΔS = 0.
S
is taken from the Ket. |
Homog
|
|
Simple homogeneous perturbation
with ΔΩ = 0; Use only if one of the other types is not appropriate.
|
aL
|
aI.L
|
Nuclear Spin Orbit perturbation
|
e
|
|
Nuclear magnetic dipole
perturbation
|
| eQq1 |
|
Nuclear electric quadrupole
perturbation |


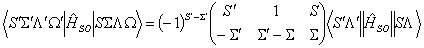
 arranged so that Λ' > Λ and Λ' > 0
(or S' > S if Λ' = Λ). It is perhaps more
normal to quote the value including the 3j
symbol, but this is ambiguous when the spin-orbit operator connects
more than one component of a pair of states. Some common non-zero
values of the 3j symbol are
tabulated below.
arranged so that Λ' > Λ and Λ' > 0
(or S' > S if Λ' = Λ). It is perhaps more
normal to quote the value including the 3j
symbol, but this is ambiguous when the spin-orbit operator connects
more than one component of a pair of states. Some common non-zero
values of the 3j symbol are
tabulated below.  term omitted from the rotational operator. The perturbation parameter
is the value of the matrix element:
term omitted from the rotational operator. The perturbation parameter
is the value of the matrix element: