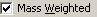l Matrix Window

This window displays, and allows the editing of, the equilibrium geometry and vibrational modes for an electronic state. To bring up the window, right click on the state and select "l Matrix...". To display a particular normal mode, click on the appropriate column. R_x, R_y and R_z are the rotations around the x, y and z axes and T_x, T_y and T_z are the translations along the axes. They are calculated from the masses and equilibrium geometries and can't be edited.

The lower panel shows the atom positions, and a normal mode motion if a mode is selected. a, b, and c are the principal inertial axes, which are calculated from the given atomic positions.
	Drag to resize the upper and lower parts.
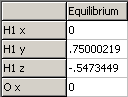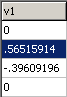
	Equilibrium positions of the atoms, in Å. These should be with respect to the centre of mass; if not see under the Operate button.
	l matrix in Cartesian co-ordinates in one of two possible forms: If "Mass Weighted" is checked the values correspond to relative atomic displacements, and the units are 1/sqrt(atomic mass units). If "Mass Weighted" is checked the values are dimensionless. In this form the matrix should be orthogonal; see under the Operate button for options to check and correct this. The conversion factor between the two for any given value is Sqrt(mass of Nucleus).
	Select plane to plot
	This controls the length of the arrows plotted on each atom to show the motion of the atom in the selected normal mode. The number is the multiple of the zero point motion, assuming the motion is harmonic.
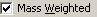	Check to show l matrix elements divided by sqrt(mass); uncheck to show as dimensionless numbers. The numbers can be edited in either mode.
	Show Translational and Rotational normal mode transformations.
	This brings up a menu with the following options: Print Geometry - Show geometrical information in the log window Fix Centre of Mass - Adjust atomic co-ordinates so centre of mass is at the origin Normalize - Adjust vibrational co-ordinates to be correctly normalized. Orthogonalize - Adjust vibrational co-ordinates to be orthogonal and correctly normalized. Also fixes centre of mass if necessary.