Molecule Types Linear Molecules <Prev Next>

Linear Molecule Perturbation

There will be one of these for each perturbation parameter in each state.

Settings

Nucleus Index, starting from 1, of the nuclear spin involved in perturbation; 0 (the default) for those not involving a nuclear spin.
SymSelect Possible values are all (normal use), e_only (only affect e levels) and f_only (only affect f levels). Was ParitySelect in previous versions.
ScalePrev Scale factor with respect to preceding perturbation
Op Perturbation type. See below for possible values. If only Npower and/or Srank, Scomp are needed, use Op = Luncouple with n = 0.
n Power of operator in perturbation.
Npower Power of N (for centrifugal distortion of perturbation). Perturbation operator is ½[N2,Op]+. If RSquaredH is set, N is replaced by R.
OmegaSelect Set to all (the default) for normal use; set to a specific value to restrict the perturbation to a specific value of Ω. Note that the current implementation applies the constraint to both connected wavefunctions, so is only useful for ΔΩ = 0 matrix elements.
Srank If Srank < 0: adds a term S±Scomp and changes the power of J or N. See the Op details below.
If Srank > 0: spherical tensor operator for S with overall rank Srank and component Scomp.
Note that both of these are only implemented for Op = Luncouple, Suncouple and LNuncouple.
Scomp

Parameters

Value Size of perturbation.
The matrix elements are described individually below, but a general comment on specifying the value of the parameter is appropriate. In a Hund’s case (a) basis there are four related matrix elements of any operator:

PGOPHER will essentially take the one in the top left as the parameter, ordering the matrix such that Λ' > Λ and Λ' > 0 (or Σ' > Σ and Σ' > 0 if Λ' = Λ or S' > S if all the other quantum numbers are equal). The two rows of the matrix can be related using the reflection operator σv:

The columns can be related by requiring the Hamiltonian to be symmetric.

Perturbation Types

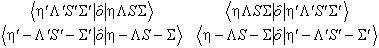
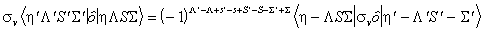
LS
Spin orbit coupling, with the Ω dependence from the Wigner-Eckart theorem; see for example Lefebvre-Brion and Field, 2nd Edition Equation 3.4.36: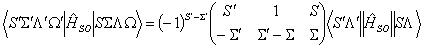

The perturbation parameter is the reduced matrix element 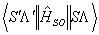arranged so that Λ' > Λ and Λ' > 0 (or S' > S if Λ' = Λ). It is perhaps more normal to quote the value including the 3j symbol, but this is ambiguous when the spin-orbit operator connects more than one component of a pair of states. Some common non-zero values of the 3j symbol are tabulated below.

S. Σ' S Σ
½ -½ ½ ½
½ ½ ½ ½
1 0 0 0
1 1 0 0
1 1 1 1
1 1 1 0


Luncouple
 		J+nL-n+J-nL+n
 L uncoupling; Using the default n = 1 this can be used to model the 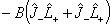term omitted from the rotational operator. The perturbation parameter is the value of the matrix element: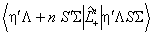

for Λ > 0 with the matrix element of L- derived by symmetry
If Srank < 0 the operator becomes: J+n+ScompS+-ScompL-n+J-n+ScompS--ScompL+n
Suncouple
 		J+nS-n+J-nS+n S uncoupling. (Note that this term with n = 1 is present in the normal Hamiltonian within a single vibronic state; it only makes sense to add it as a perturbation between states.) It checks for ΔΛ = 0 and |ΔΣ| = n, but does not check for ΔS = 0. S is taken from the Ket. (Note this form is not useful with Srank < 0).
Homog
Simple homogeneous perturbation with ΔΩ = 0 selection rule; Use only if one of the other types is not appropriate.
NS
N.S (n is ignored)
RS
R.S (n is ignored)
LNuncouple
 N+nL-n+N-nL+n Similar to Luncouple, but with J replaced by N.
If Srank < 0 the operator becomes: N+n+ScompS+-ScompL-n+N-n+ScompS--ScompL+n
aL
 		aI.L
 Nuclear Spin Orbit perturbation
e
Nuclear magnetic dipole perturbation
eQq1
Nuclear electric quadrupole perturbation

Rotational Hamiltonian expressed as perturbations

The standard rotational Hamiltonian can be expressed entirely in terms of diagonal perturbations, as shown in the table below. The scale factor indicates the factor the standard parameter must be multiplied by to use the given perturbation. This is useful as it allows additional terms to be added, such as higher powers of the centrifugal distortion terms or alternative forms of the lambda doubling to be added. Note that the "Op" is irrelevant if n = 0, but Luncouple should be used in this case.
Name
 Operator
 Op
 n
 Npower
 Srank
 Scomp
 Scale
Factor
 Notes
B N2
 (Luncouple) 0 2 0 0 1 N2 is replaced by R2 if RSquaredH is set
D N4 (Luncouple) 0 4 0 0 -1 N4 is replaced by R4 if RSquaredH is set
H N6 (Luncouple) 0 6 0 0 1 N6 is replaced by R6 if RSquaredH is set
L N8 (Luncouple) 0 8 0 0 1 N8 is replaced by R8 if RSquaredH is set
M N10 (Luncouple) 0 10 0 0 1 N10 is replaced by R10 if RSquaredH is set
PP N12 (Luncouple) 0 12 0 0 1 N12 is replaced by R12 if RSquaredH is set
A see above
 LS 1 0 0 0 Scale factor calculated to give LzSz operator form
AD see above
 LS 1 2 0 0 Scale factor calculated to give ½[N2,LzSz]+ operator form
gamma N.S
 NS 1 0 0 0 1
gammaD ½[N2,N.S]+ NS 1 2 0 0 1 N2 (only) is replaced by R2 if RSquaredH is set
gammaH ½[N4,N.S]+ NS 1 4 0 0 1 N4 (only) is replaced by R4 if RSquaredH is set
gammaL ½[N6,N.S]+ NS 1 6 0 0 1 N6 (only) is replaced by R6 if RSquaredH is set
LambdaSS 6-½(3Sz2-S2) (Luncouple) 0 0 2
 0 (8/3)½
LambdaD ½[N2,6-½(3Sz2-S2)]+ (Luncouple) 0 2 2
 0 (8/3)½ N2 (only) is replaced by R2 if RSquaredH is set
LambdaH ½[N4,6-½(3Sz2-S2)]+ (Luncouple) 0 4 2
 0 (8/3)½ N4 (only) is replaced by R4 if RSquaredH is set
theta 280-½(35Sz4-20S2Sz2+25Sz2-6S2+3S4) (Luncouple) 0 0 4
 0 (35/18)½

Lambda doubling for Π states

For all of these operators, the N is replaced by R if RSquaredH is set; the N+ and N- operators are not changed.

Name
 Operator
 Op
 n
 Npower
 Srank
 Scomp
 Scale
Factor
o S+2L-2+S-2L+2 LNuncouple 2 0 -1 -4 ½
oD ½[N2,S+2L-2+S-2L+2]+ LNuncouple 2 2 -1 -4 ½
oH ½[N4,S+2L-2+S-2L+2]+ LNuncouple 2 4 -1 -4 ½
oL ½[N6,S+2L-2+S-2L+2]+ LNuncouple 2 6 -1 -4 ½
p N+S+L-2+N-S-L+2 LNuncouple 2 0 -1 -2 -½
pD ½[N2,N+S+L-2+N-S-L+2]+ LNuncouple 2 2 -1 -2 -½
pH ½[N4,N+S+L-2+N-S-L+2]+ LNuncouple 2 4 -1 -2 -½
pL ½[N6,N+S+L-2+N-S-L+2]+ LNuncouple 2 6 -1 -2 -½
q N+2L-2+N-2L+2 LNuncouple 2 0 0 0 ½
qD ½[N2,N+2L-2+N-2L+2]+ LNuncouple 2 2 0 0 ½
qH ½[N4,N+2L-2+N-2L+2]+ LNuncouple 2 4 0 0 ½
qL ½[N6,N+2L-2+N-2L+2]+ LNuncouple 2 6 0 0 ½

An alternative form for these operators, used in some circumstances, can be obtained by replacing LNuncouple with Luncouple. This has the effect of replacing N+ and N- with J+ and J- throughout. For example the p + 2q is the determinable constant in some circumstances, and corresponds to the operator ½(J+S+L-2+J-S-L+2). This can be created from the perturbation corresponding to "p" above, with Op = Luncouple, n = 2, Srank = -1 and Scomp = -2.

Lambda doubling for Δ and higher states

A few lambda doubling operators for Δ states are built into PGOPHER, though note that these use the form involving J rather than N, and the name is not standard for some of them. The form involving N can be obtained by replacing Luncouple with LNuncouple and lambda operators for higher values of Λ can be obtained by setting n = 2Λ.

Name
 Operator
 Op
 n
 NPower
 Srank
 Scomp
 Scale
Factor
 Notes
o S+4L-4+S-4L+4 Luncouple 4 0 -1 -8 ½ The conventional name would be m
oD J+S+3L-4+J-S-3L+4 Luncouple 4 0 -1 -6 -½ The conventional name would be n
oH J+2S+2L-4+J-2S-2L+4 Luncouple 4 0 -1 -4 ½ The conventional name would be o
p J+3S+L-4+J-3S-L+4 Luncouple 4 0 -1 -2 -½
q J+4L-4+J-4L+4 Luncouple 4 0 0 0 ½