Asymmetric Top Hamiltonian

The asymmetric top Hamiltonian used is either of the A or S standard reduced forms proposed by Watson (Watson, 1977). The SReduction flag at the Molecule level determines which one, with a setting of false implying the A reduction is used. When reporting these constants it is important to specify both the reduction and the axis system used. Note that, for open shell systems with S > 0, J should be replaced with N in the discussion below, though not in the parameter names.

The rigid rotor part can be specified in two ways, independent of the reduction:
or the equivalent form (which can give better determined parameters):
where:
and:
Note that this alternate form, as currently implemented, requires the a and z axes to be same, i.e. for a Ir or Il representation to be used.

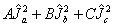
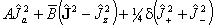
The different forms of the centrifugal distortion terms do not have a simple relationship:

	A reduction
Quartic
Sextic
Octic

	S reduction
Quartic
Sextic
Octic

Note that various symbols are in use for many of the centrifugal distortion constants; in particular different symbols are typically used for the A and S reduction constants rather than as here. Some of these are listed below, together with the name PGOPHER uses.

PGOPHER	A reduction	S reduction
A	A
B	B
C	C
BBar
Bdelta
DJ	ΔJ	DJ
DJK	ΔJK	DJK
DK	ΔK	DK
deltaJ	δJ	d1
deltaK	δK	d2
HJ	ΦJ	HJ
HJK	ΦJK	HJK
HKJ	ΦKJ	HKJ
HK	ΦK	HK
phiJ	φJ	h1
phiJK	φJK	h2
phiK	φK	h3
LJ	LJ
LJJK	LJJK
LJK	LJK
LKKJ	LKKJ
LK	LK
llJ	lJ
llJK	lJK
llKJ	lKJ
llK	lK

Open Shell Molecules

For open shell molecules (S > 0) a Hund’s case (b) basis is used. The rotational part is as above, though for J and its components read N throughout. The following additional terms are present:

Spin Rotation Interaction

ε_aaN_aS_a +  ε_bbN_bS_b +  ε_ccN_cS_c
+ ½ε‾_ab(N_aS_b + S_bN_a + N_bS_a + S_aN_b)
+ ½ε‾_ac(N_aS_c + S_cN_a + N_cS_a + S_aN_c)
+ ½ε‾_bc(N_bS_c + S_cN_b + N_cS_b + S_aN_b)

where ε‾_ab = eabbar = ½(ε_ab + ε_ba), ε‾_ac = eacbar = ½(ε_ac + ε_ca) and ε‾_bc = ebcbar = ½(ε_bc + ε_cb). The slightly long winded form arises because the operators N_p and S_q only commute if p = q. Following Brown and Sears (1979) the centrifugal terms come in two slightly different forms, depending on the representation:

A reduction:	ΔsNN2N.S + ½ΔsNK(N2NzSz+NzSzN2) + ΔsKNN.SNz2 + δsNN.S(N+2 + N-2) + ½δsK{(N+2 + N-2)NzSz + NzSz(N+2 + N-2)}
S reduction:	DsNN2N.S + ½DsNK(N2NzSz+NzSzN2) + DsKNN.SNz2 + ds1N.S(N+2 + N-2) + ds2(N+3S+ + N-3S-)

Only that last term actually has a different operator form. Note that the S reduction names are used to label the parameters. 

Spin Spin Interaction

α(3S_z²-S²) + β(S_x²-S_y²)

Also in use are D = 3α and E = β.

References

• J. M. Brown and T. J. Sears, "A reduced form of the spin-rotation Hamiltonian for asymmetric top molecules, with applications to HO₂ and NH₂, J. Mol. Spec. 75, 111 1979.
  
• J. K. G. Watson in "Vibrational Spectra and Structure" (Ed: J. Durig) Vol 6 p 1, Elsevier, Amsterdam, 1977.