Molecule Types Vibrational Structure Force Field Analysis <Prev Next>

Symmetry Coordinates

Symmetry coordinates, S, are specified by giving the transformation matrix, U, between S and the internal coordinates, R:

S = U R = U B Δx

The symmetry coordinates window, shown below for C2H4, allows the display and editing of the U matrix and (optionally) the force field in terms of symmetry coordinates, F. To create a symmetry coordinates object, right click on the Electronic State object object and select "Add New..., Symmetry Coords". To bring up the window right click on the symmetry coordinates object and select "View...". If a symmetry coordinates object is not present, or the U matrix is left blank, an identity matrix is assumed for the U matrix. Note that the current version of the program ignores the point group set for the molecule as a whole, and the symmetry set for the individual vibrational modes when doing the force field calculation. This may be changed in future versions of the program.


The Controls

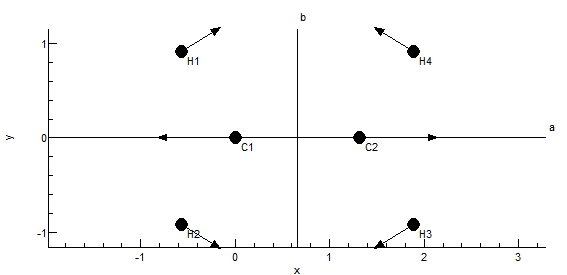
The plot at the bottom shows the current symmetry coordinate, i.e. the selected row in the top left grid. The arrows indicate how far each atom moves. The plot updates semi-automatically; use "Operate, Check" to force an update.

G
+
PlotPlaneGroup The "Plot Plane" control allows the selection of the plane in which to plot the molecule.
MagnificationSpinThe magnification selects the scale factor to use for the arrows.
StatusBar The status bar shows the latest mouse position; draw a box with the mouse to measure distance and angles.
OperateButton
The operate button brings up a menu of possible operations:
Check
 		Check the contents of the top grids, and update the plot to match
Apply
 		Check the contents of the top grids, and display the details of the vibrational mode calculation in the Log Window. This also forces other objects to update.
Show F Matrix Print the F matrix in the Log Window calculated from the l matrix elements and frequencies given in the vibrational mode objects. The transformation is done by calculating the matrix L, which relates the symmetry coordinates, S, and normal coordinates, Q:
S = L Q
The L matrix is available from:
L = U B M-½ l
providing the internal coordinates are fully specified and the F matrix can then be calculated from:
F = (L-1)T λ L-1
Note that the U matrix is not necessarily required, but if there are redundant internal coordinates L-1 can't be calculated. In this case an alternative relationship can be used:
F = L λ LT
provided that L LT= 1.
Set F Matrix Clear the f matrix grid (top right) and set it from the l matrix elements and frequencies given in the vibrational mode objects. See the entry above for details of the calculation.
Sort F Matrix by Value Sort the F matrix grid (top right) in descending order of the first column.
Sort F Matrix by Mode Sort the F matrix grid (top right) by mode numbers, with diagonal elements first.

The Force Constant Matrix

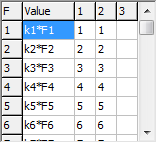
FGrid
The grid at the top right allows the force field to be given in terms of valence coordinates:

V = ½ ST F S = ½ Σij FijSiSj

The non zero elements of the F matrix, Fij are specified in the grid, with the force constant in the first column, and i and j in the next two columns. (The fourth column is to allow future expansion to cubic and higher terms.) The force constants can be given as simple numerical values, but can also be given as general expressions involving symbolic values. This is typically more useful as it allows, for example, relationships between isotopologues to be added naturally. For the example shown here the constants are expressed as the product of two factors, such as k2*F2. The intent is that k2 is a scaling factor, as commonly used in interpreting ab initio calculations; here a different scaling factor is used for each mode, but an obvious change would allow the same scaling factor to be used for each mode. When reading the force constant matrix, unknown variables are automatically created as parameters to the current internal coordinates object, and they can then be edited in the Constants Window. If dealing with more than one isotopologue, these variables are better placed in a variables object, (with Global set to true) so the same value can be used in all species.

Note that the force constant grid will expand automatically as atoms are added. The grid can be left blank if the potential energy is to be expressed in terms of internal coordinates.

Symmetry Coordinates

Grid
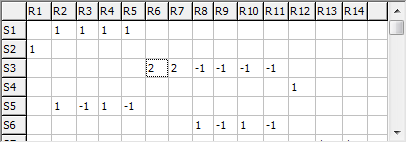
The grid at the top right allows the U matrix to be specified; each row corresponds to a specific symmetry coordinate, and the column the contribution from each internal valence (R) or Cartesian (B) coordinate. As for the other matrices, either a simple numerical value or a symbolic expression can be entered.

Internal Coordinates Settings

Active Set true to use this symmetry coordinates object; there must be no more than one active symmetry coordinates object at a time.
Normalize If true, the rows of the matrix given are normalized before use in further calculations
PreserveS
 If true, the normal modes are in the same order as the symmetry coordinates, using the largest coefficients in the L matrix to align the two. This is not guaranteed to work, particularly if there is significant mixing between the symmetry coordinates.
If false, the normal modes are sorted by energy.
Note that the current version of the program ignores the point group set for the molecule as a whole, and the symmetry set for the individual vibrational modes when doing the force field calculation. This may be changed in future versions of the program.