The pure rotational spectrum of the ground state of NH3/ND3
and the Stark effect
NH3
The data files given here were
constructed by fitting to the line positions and intensities in
the HITRAN 2008 (http://www.hitran.com)
database. The fit was restricted to J < 16, and is sufficient to reproduce the
line positions to better than 0.001 cm-1 and the
intensities to better than 10-20 cm2 cm-1 Molecule-1.
There are two points that are slightly non-standard:
- The point group used is D3h, rather than C3v.
This is necessary to account for the inversion doubling in the
ground state, which appears in the data file as two vibrational
states:
- s/0+ with A1'
symmetry
- a/0- with A2"
symmetry
- To fit the K = 3n
levels requires three perturbation
operators:
- <0+|J+-^6|0+>
= J+6 + J-6
- <0+|J^2J+-^6|0+>
= J2(J+6
+ J-6)
- <0+|J+-^12|0+>
= J+12 + J-12
Two separate data files are
provided, with the required constants. The first is
nh3x0.pgo which has the two
inversion doublets in separate manifolds (s and a), with a
transition moment acting between the two manifolds. This is a good
starting point for simulating electronic spectra, where the
transitions will typically be from one inversion doublet or other.
The Stark Effect
The second file,
nh3x0one.pgo, has the same
constants in, but with the two inversion doublets in the same
manifold. The resulting energy levels will be the same, but as the
dipole moment now acts within the manifold, the Stark effect in
the ground state can be simulated with this file. To give quick
calculation times Jmax has been set to 5 for this file. The
energy level plot window can then be
used to produce a plot of energy against field, as for example:
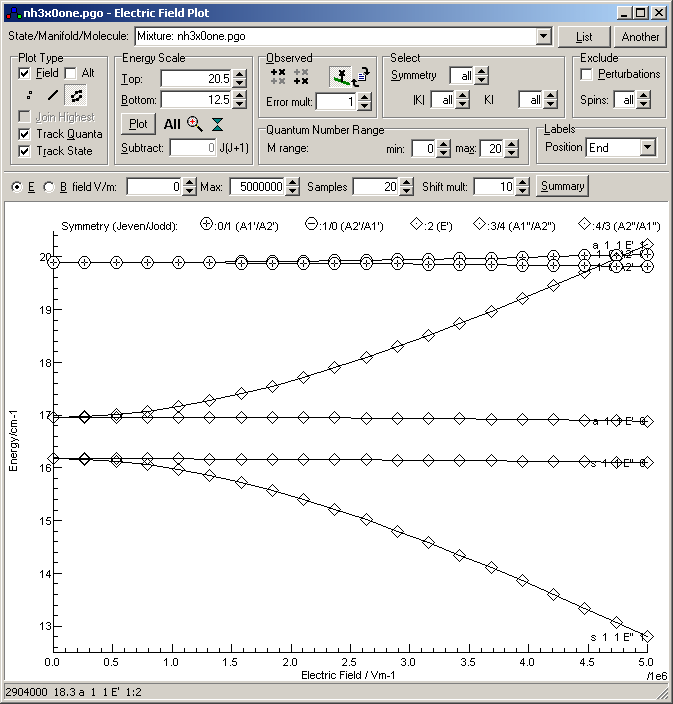
This shows the K = 1, M = 1 levels show a strong
Stark effect, but the other levels show a rather weaker effect.
The "Summary" button gives the following information:
M Sym # g Population Name J K (kl) Sym M Energy Linear Dipole Err Quadratic Err Two Level Delta C Dipole2 Err
0 - 1 4 .660533316 a 0 0 A2" 0 0.7933 -5.20523347e-9 -.0309983 15.8% -1.0409798e-15 .02 %
0 - 2 2 .036129526 s 1 1 E" 0 16.1730 -1.47243024e-9 -.0087686 15.8% -2.9448374e-16 .002%
0 - 3 2 .032246486 a 1 1 E' 0 16.9632 -1.53137719e-9 -.0091197 15.8% -3.0627282e-16 .002%
0 - 4 4 .042329414 s 1 0 A2' 0 19.8899 3.241105275e-9 .01930147 15.8% 6.48153456e-16 .033%
1 - 1 2 .036129526 s 1 1 E" 1 16.1730 -7.02797997e-8 -.4185312 13.9% -1.3786935e-14 5.18% 16.583449 .82098935 -1.25126674e-7 -.7451561 .013%
1 - 2 2 .032246486 a 1 1 E' 1 16.9632 6.802667704e-8 .40511341 13.9% 1.33363101e-14 5.36% 16.583784 .75886528 1.190970869e-7 .70924861 .015%
1 - 3 4 .042329414 s 1 0 A2' 1 19.8899 -1.47290548e-9 -.0087715 15.8% -2.9457878e-16 .002%
This indicates that the K
= 1 levels are intermediate between a first and second order Stark
effect, and the others are essentially showing a second order
(quadratic) Stark effect. See External
Fields - The Zeeman and Stark Effects for more information.
ND3
A similar set of data files for ND3 is given below. The
data sources are L Fusina and S N Murzin, J. Molec. Spectrosc. 167 464 (1994), L H Coudert and
E Roueff, Astron. Astrophys. 449
855 (2006) and the ND3
linelist from the Cologne Database for
Molecular Spectroscopy (CDMS).
-
nd3x0.pgo,
similar to the nh3x0.pgo file above. This was derived by from
an unweighted fit to all lines in the CDMS linelist with
J < 16, which gave an
average error of 7×10
-5 cm
-1 and a
maximum error of 0.003 cm
-1. This has the two
ground state inversion doublets in different manifolds, giving
a simpler description than in the next file.
-
nd3x0one.pgo,
equivalent to the nh3x0one.pgo file above, with both ground
state inversion doublets in the same manifold to allow the
Stark effect to be simulated. This uses exactly the
Hamiltonian and constants used in the Fusina and Murzin paper.
This includes perturbations acting between the two inversion
doublets, though note that the sign of the α
J and α
K constants must
be changed in
PGOPHER
to give consistent matrix elements. The line positions agree
with the CDMS linelist to < 0.006 cm
-1 (
<
0.0005 cm-1 for J < 15). The operators mixing states
are:
- <0-|JzJ+-^3|0+>
= [J+3 + J-3, Jz]+
(term in α)
- <0+|J^2JzJ+-^3|0+>
= J2[J+3
+ J-3, Jz]+ (-term
in αJ)
- <0+|Jz^3J+-^3|0+>
= [J+3 + J-3, Jz3]+
(-term in αK)
-
nd3x0hyp.pgo
which has the hyperfine structure due to the nitrogen nucleus
added to the simulation, giving a linelist consistent with the
Coudert and Roueff paper.
