| <Prev Next> |
| For all states | 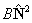 |
Rotation |
| S > 0 | 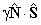 |
Spin-Rotation |
| Λ > 0, S > 0 | 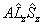 |
Spin-Orbit |
| S > 1/2 | 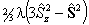 |
Spin-Spin |
| S > 1 |
Spin-Rotation | |
| Λ > 0, S > 1 |
Spin-Orbit | |
| S > 3/2 | 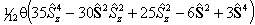 |
Spin-Spin |
| Π states | 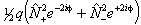 |
Λ doubling |
| Π states, S > 0 | 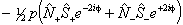 |
Λ doubling |
| Π states, S > 1/2 | 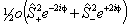 |
Λ doubling |
| Δ states |
See Λ type doubling for
Δ and higher states. |
|
See the individual sections below for a more detailed discussion. Note that any operators not listed above (such as alternate forms of operators or higher powers of centrifugal distortion) can be generated using a perturbation diagonal in electronic state.
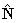 :
:
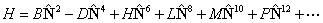
though formally, it should only involve the rotational angular
momentum of the nuclear framework, 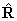 and thus be written:
and thus be written:
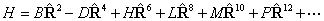
PGOPHER can use
either form, as controlled by the "RSquaredH" flag at the molecule
level. This flag affects many of the terms in the Hamiltonian; for
all the linear molecule terms read 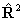 for
for 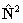 if RSquaredH=True; to follow the
IUPAC recommendations the
if RSquaredH=True; to follow the
IUPAC recommendations the 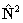 form must be used.
form must be used.
The reason both forms are in use is that each has some problems
in evaluation, as discussed by Brown et al, 1987. Strictly
the second form is correct, but full evaluation is not possible
because of the terms involving 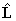 .
Consider evaluating the
.
Consider evaluating the 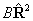 term:
term:
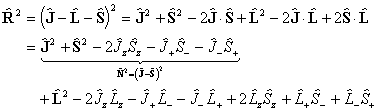
The diagonal terms are:
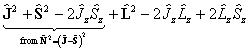
which becomes:
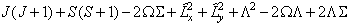
The 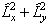 term
must be discarded, leaving:
term
must be discarded, leaving:
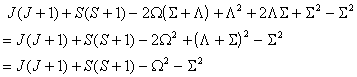
which is the form used. The equivalent expression in  is:
is:
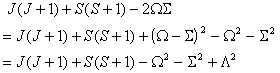
i.e. simply an additional Λ2
term compared to 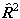 . The main
practical difference is a shift in the effective band origin of BΛ2
(so they are identical for Σ states), but it is not clear
that one is any more correct than the other as both ignore the
term
. The main
practical difference is a shift in the effective band origin of BΛ2
(so they are identical for Σ states), but it is not clear
that one is any more correct than the other as both ignore the
term 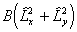 .
This latter term is only likely to be worth considering if isotope
shifts of vibrational band origins are required, and the former
leads to different definitions of the band origin, so it is worth
checking all published constants to see which is used. The matrix
elements of higher powers of
.
This latter term is only likely to be worth considering if isotope
shifts of vibrational band origins are required, and the former
leads to different definitions of the band origin, so it is worth
checking all published constants to see which is used. The matrix
elements of higher powers of 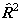 or
or 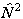 are evaluated by
evaluating the matrix of
are evaluated by
evaluating the matrix of 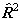 or
or
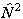 as above and taking the
appropriate power of the matrix. This means that the RSquaredH flag will cause
small changes which will affect most of the constants so, for
example, B will change by 2Λ2D.
as above and taking the
appropriate power of the matrix. This means that the RSquaredH flag will cause
small changes which will affect most of the constants so, for
example, B will change by 2Λ2D.
Of the off-diagonal terms, ![]() is the same in both forms, and
their inclusion allows Hund's case (b) to be accurately modelled.
The terms off diagonal in Λ:
is the same in both forms, and
their inclusion allows Hund's case (b) to be accurately modelled.
The terms off diagonal in Λ:
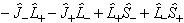
are normally discarded in both forms of the Hamiltonian as they only connect completely different electronic states so they are not normally important. They can be included as a perturbation if required (see Luncouple)
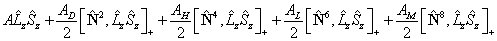
where:
![]()
Note that, for 2Π states AD and the spin rotation constant γ (see below) have the same effect on the energy levels so their effects can only be distinguished by special methods (Veseth, 1971 and Brown and Watson, 1977). For this reason only one of AD and γ is normally used. A similar equivalence applies in practice for higher order centrifugal distortion terms, so these were only implemented in 10.1.158. Any required centrifugal term can be generated using perturbations if required.
For states with S > 1 an additional term is required:
![]()
as described in Brown et al, 1981.
For S > 1/2 the spin-spin interaction can contribute:
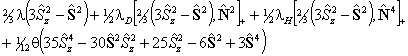
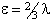 is also in use. The term
in θ only contributes for states with S > 3/2;
again see references in Brown et al, 1987. Read
is also in use. The term
in θ only contributes for states with S > 3/2;
again see references in Brown et al, 1987. Read 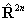 for
for 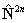 if RSquaredH=True.
if RSquaredH=True.
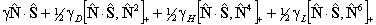
If RSquaredH=True, read 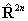 for
for 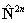 but note the
but note the 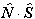 term is unchanged. For S
> 1 an additional term is also required:
term is unchanged. For S
> 1 an additional term is also required:
![]()
The IUPAC form is:
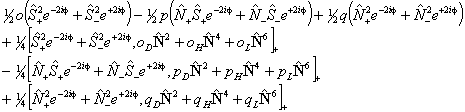
Of these terms q will contribute for any Π state; for 1Π states it is effectively the difference between the rotational constants for e and f parity states. p requires S > 0 also and o will only contribute for S > 1/2. The e±2iφ terms are shorthand to ensure that the Λ-doubling operators only connect the two halves of a Π state:
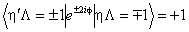
If RSquaredH=True, read 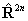 for
for
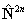 in the centrifugal distortion
terms, and leave the other operators unchanged. There are
alternative Λ doubling parameters, in use including:
in the centrifugal distortion
terms, and leave the other operators unchanged. There are
alternative Λ doubling parameters, in use including:
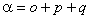
This arises naturally from expressing the Hamiltonian in terms of
J, rather than N as can be seen by making the
replacement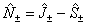 :
:
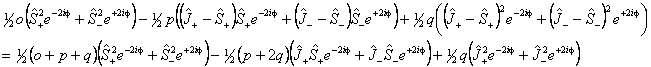
See Brown and Merer, 1979 for a discussion of this. This also
explains why under some circumstances only p + 2q
is determined rather than p and q individually. (A
term equivalent to this can be generated using perturbations;
see the CrO sample file for an example of
this.)
Λ doubling in Δ states is discussed by Brown et al, 1987. They propose two different forms, a case (b) form:
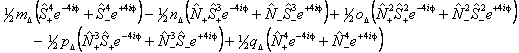
and a case (a) form:
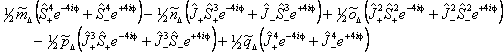
The case (a) form is programmed into PGOPHER with the non-standard names for the parameters: m̃Δ = o, ñΔ = oD, õΔ = oH, p̃Δ = p and q̃Δ = q, but does not include any centrifugal distortion terms. The case (b) form, and centrifugal distortion of either can be generated using perturbation objects, and Λ doubling operators for higher values of Λ can also be generated in this way.