Procedures Details | Procedures Details |
<Prev Next> |
A reasonably general way to write the term in the Hamiltonian arising from the interaction of a molecule with an external electric field is of the form:
This is written in spherical tensor form, with k being the rank of the tensors involved. p is a projection quantum number (|p| ≤ k), reflecting the projection of a tensor of rank k onto the space fixed z axis. Limiting the sum to k = 1 corresponds to the common electric dipole case, in which case T1(μ) is the electric dipole moment operator (in a space fixed frame) and T1(E) is the electric field. The Zeeman Hamiltonian is similar, with electric field (E) replaced by magnetic field (B) and the electric dipole being replaced by the magnetic dipole. More exotic transitions can have contributions from other ranks, including Raman (typically k = 0 and 2), quadrupole (k = 2) and multiphoton (k ≤ number of photons) transitions. For all these cases the matrix element of the above operator is required to calculate intensities of transitions and shifts in external fields, which can be written as:
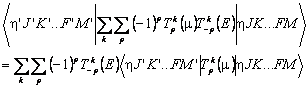
…F implies various the spin angular momenta adding up to F, though these will be absent in the simplest cases with no spins where J = F. We use K to illustrate the handling of molecule fixed quantum numbers; for linear molecules read this as Ω instead of K. η is used to represent all the vibrational and electronic quantum numbers, apart from electronic spin; in PGOPHER this essentially corresponds to the identity of the state object.
The field, Tk(E), is constant, so we only require the matrix elements of the dipole moment, Tk(μ), the transition moment. The details of the matrix element will depend on the molecule, though F (the total angular momentum) and M (its projection along the space fixed z axis) will be present in all cases. The first step in evaluating this matrix element is the Wigner-Eckart theorem:
Assuming Tk(μ) does not operate on the spin parts (though it could for the Zeeman Hamiltonian) we have the following for a single spin with F = F1 + I:
with a similar multiplying factor for the reduced matrix element introduced for each additional spin. To evaluate the last term on the right hand side we must transform the operator from space to body fixed components. This can be done using Wigner D matrices:
where q is used to label the projections of the tensor onto the body fixed axis system. The matrix element with all the spins removed is:
corresponds
to
the
(transition)
dipole
moment
in the body fixed axis system, and its numerical value corresponds
directly to the value input when using a spherical transition
moment. For calculating Stark and Zeeman shifts the above
equations (adapted as required for additional quantum numbers) can
be used directly to evaluate the required matrix elements for the
overall Hamiltonian matrix.
The intensity of a transition is proportional to the square of the transition moment worked out above. Two steps are required for this. Firstly, the above expresses the matrix element in terms of the basis states, but a transformation to the true states using the eigenvectors from the matrix diagonalization to find the energy levels is required. (This is molecule specific, so is not discussed further here, but complicates the situation in cases like asymmetric tops and linear molecules that are not a pure Hund's case (a), where the line strength will involve a linear combination of the transition moments above.) Secondly, in the absence of external fields, the different M levels are degenerate, so the sum over all possible transitions between the degenerate upper and lower state levels is required. This leads naturally to the definition of the line strength, S, in the literature:
The sum over p corresponds to the sum over possible polarisations of the light; under standard conditions, such as spontaneous fluorescence, the unweighted sum as above is appropriate. However, to allow PGOPHER to handle relative intensities between different ranks of transitions in multiphoton spectroscopy, a different line strength is introduced, Spol, defined as the sum over upper and lower state M for a single polarization, p = 0:
With this definition of Spol, the contributions from different ranks of transition moment tensor in a multiphoton spectrum can simply be added together, assuming linearly polarised light is used. (Different weighting factors must be used for circularly polarized light.)
The standard line strength for one photon transitions comes from summing over the 2k+1 components. These must be independent of polarization (as spontaneous fluorescence is unpolarized) which gives:
This also implies S = 3 Spol for single photon transitions.
For quantitative calculations of absorption cross-section this has units, specifically the square of the units used for the value in the transition moment object. The built in conversions (see below) assume Debye for electric dipole (transition) moments and Bohr or nuclear magneton for magnetic dipole moments.
The line strengths, S, are also Hönl-London factors, with some caveats. Consider a simple parallel transition in a singlet state of a linear molecule. This has J = F, K = Λ and the above equations give:
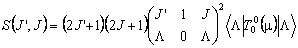
For R branch transitions within a Σ state, J' = J + 1 and Λ = 0 so the above becomes:
For an R branch of a perpendicular Π – Σ band:
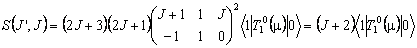
The Hönl-London factors are J + 1 and J + 2 respectively, so Hönl-London factors can be obtained by setting the transition moment value(s) to 1 provided there is only a single transition moment contributing to any given transition.To find the Hönl-London factor for a particular transition given this setup, set the IntensityUnits of the simulation to HonlLondon before simulating; in the linelist window obtained by right clicking on a transition the "Strength" column will then be the Hönl-London factor.
Caveats: The number displayed is simply 3 Spol as defined above, so is correct for single photon transitions, but care must be taken for multiphoton transitions. For ranks (k) other than one a scaling by (2k+1)/3 is in principle appropriate, but it depends on the polarization of the light. As discussed above, for linear polarization the Spol values must be added, rather than S, and a different rule is required for circularly polarized light. In addition, setting the transition moments to 1 may not be possible if more than one molecular transition moment contributes to a given transition, as the relative signs and magnitudes will affect the computed value for Spol. In particular quantum mechanical interference can take place so, for example, if two transition moments contribute, setting both to +1 will typically give a completely different spectrum to values of +1 and –1.
The transitions window displays the make up of Spol but can, for simpler cases, be switched to show S. The default is to display:
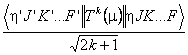
i.e. Spol1/2 - note the inclusion of the 2k+1 factor. If a only a single transition moment is involved in the selected transitions, or all the transition moments have the same rank, then a Hönl-London check box will be enabled and checking it will remove the 2k+1 factor.
The “original” transition matrix pane shows the above matrix element between the basis states contributing to the selected total angular momenta and symmetries. The “transformed” transition matrix comes by transforming the original matrix with the eigenvectors from the matrix diagonalization for the two manifolds involved. The transformation must be done before the matrix elements are squared to allow for interference between transition moments.
Note that this reduced matrix is not necessarily symmetric. This can be seen by considering:
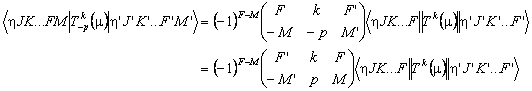
Considering p = 0 specifically we expect:
and comparing equations implies
Reduced matrix elements off diagonal in total angular momentum by an odd integer will therefore change sign, depending on the order chosen. This is harmless for intensity calculations, and field calculations will include the full matrix element anyway.