Molecule Types Vibrational Structure Vibrational Energy Levels and Franck-Condon Factors <Prev Next>

Worked Example - The Photoelectron Spectrum of H2O

The key parameters required for a simulation of a vibrational spectrum are summarized in Making a basic data file for simulating vibrational structure. The steps below show how to do this for the first band in the photoelectron spectrum of water, using literature values for constants where available. See the related worked example, Predicting the Photoelectron Spectrum of H2O using ab inito Calculations for an alternative approach.

The Constants

An excellent compilation of spectroscopy constants for can be found in the NIST Chemistry web book at  http://webbook.nist.gov/chemistry/. A formula search on H2O with ions not excluded yields information on several isotopes; selecting the main isotope and then "Vibrational and/or electronic energy levels" yields for H2O:

Sym
Species
 No Approximate
type of mode
 Selected
Freq
a1
 1
 Sym str
 3657
a1
 2
 Bend
 1595
b1
 3
 Anti str
 3756

Confusingly the asymmetric stretch, v3, is shown as having b1 symmetry in this table, though the modern convention is to classify this mode as b2. The b2 symmetry follows if the out of plane axis is chosen to be the x axis, the current convention, while b1 symmetry follows if the out of plane axis is chosen to be the y axis. The choice is not necessarily important for the simulation, but it is important to be consistent.

Selecting "Gas phase ion energetics data" gives an ionization potential of 12.621 eV; see below for some discussion of this value.

For the ion information on several states is available; taking just the most recent ground state (X state) gas phase values:

Vib
Sym
 No Approximate
type of mode
 cm-1
a1
 1
 Sym stretch
 3197.97
a1
 2
 Bend
 1408.42
b2
 3
 Asym Stretch
 3253.91

Note that the asymmetric stretch is shown as b2 here. More detailed simulations would have to consider anharmonicities.

Setting up the simulation

There is now enough information to produce a basic simulation in PGOPHER:
  1. Click on File, New, Vibrational Spectrum.
  2. Select View, Constants
  3. Click on "VibratingMolecule". This sets the parameters common to all states, and the ones that need to be changed from the default values are:
    1. PointGroup = "C2v"
    2. nModes = 3. This is the number of vibrational modes. Note that you should not set the number of atoms (nNuclei) unless you want to input an l matrix for each state.
  4. No changes need to be made at the manifold level for the neutral, "Ground", though you may want to rename it to "Neutral", by right clicking on it and selecting "Rename".
  5. Click on each mode in the neutral ground state in turn (v1, v2 and v3 under X) and enter:
    1. Omega - the frequency from the first table above.
    2. Symmetry - the symmetry of the mode, which you will only need to change for the asymmetric stretch, v3.
    3. vMax = 0. This selects the maximum vibrational quantum number to be considered in each mode. The default (3 or 5) will lead to rather a slow simulation; setting to 0 means that vibrationally excited states are excluded.
  6. The manifold labeled "Excited" corresponds to the ion; no changes need to be made here, though you may want to rename it to "Ion".
  7. Click on the ion ground state, "A" and set:
    1.  Symmetry = B1 - the symmetry of the electronic ground state of the ion.
    2.  Origin = 101795 cm-1 = 12.621 eV. This is the energy of the ground state of the ion with respect to that of the ground state of the neutral, the ionization energy. (Strictly this is the difference in energy between the minima of the potential energy curves for the two states.) Tip: to avoid having to convert the value from eV, click on the Convert Units button until the units show "eV", enter the value in eV and then click on the button again until cm-1 appears.
    3. You may want to rename the state to X or perhaps IonX, as it is the ground state of the ion, rather than the A state.
    4. The spin, S should be left as zero rather than ½ as PGOPHER does not have a specific calculation mode for ionization. Ignoring spin effects will be a reasonable approximation unless spin splittings are large.
  8. Click on each mode in the ion ground state in turn (v1, v2 and v3) and enter:
    1. Omega - the frequency from the second table above.
    2. (The symmetry will have been set in step 5.2 above.)
    3. Leave vMax as the default here; you may need to adjust this depending on the length of the vibrational progressions.
  9. The default geometry change is too large; as the ionization here is from a non-bonding orbital an initial assumption of no change would be more reasonable. Click on each normal mode under the multidimensional Franck-Condon factor, <IonX|FCF|X> and ensure:
    1. Displacement = 0. This represents the change in each normal mode.

This should be enough for a basic simulation; press the simulate button (Simulate) and then the all button (all) and you should see a simulation, though it will essentially have only one peak as we are assuming no geometry change on ionization.

Checking and refining the simulation

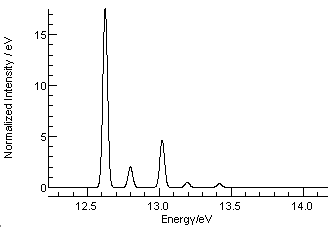
    It is important to check simulations, not only because it is easy to make mistakes in the steps above, but also because there can be differences in the definitions of the constants or other factors, such as the different choice of symmetry for the asymmetric stretch described above. Checking against tabulated line positions or published spectra is an effective check; note the facility for overlaying pictures (from a Journal for example) onto a simulation.

    In this case an experimental simulation is available from R. N. Dixon, G. Duxbury, J. W. Rabalais and L. Åsbrink, "Ro-vibronic structure in the photoelectron spectra of H2O, D2O and HDO", Molecular Physics, 31, 423, http://dx.doi.org/10.1080/00268977600100311. This shows that, while the first peak is indeed the strongest, about ¼ of the intensity is in the other peaks. Manually adjusting the vibrational displacements to v1 = 0.07, v2 = 0.07 gives a reasonable match for the observed intensities. As a final point, the peaks are all shifted from the simulation - the strongest peak is simulated at 12.550 eV but measured at 12.624 eV. The difference here (0.074) is likely to be the zero point energy; this could be checked by looking at the individual vibrational levels - selecting "View", "States".  Adding 0.074eV = 600 cm-1 to the ion origin brings the spectra into line, as shown in the plot below.

H2O PES simulation

To obtain the plot the plot units were set to eV ("Plot", "Units", "eV") and a Gaussian width of 0.04 eV was selected (The "Gau" box on the main window toolbar). The completed file is available as H2OPES.pgo.