Molecule Types Vibrational Structure Force Field Analysis <Prev Next>

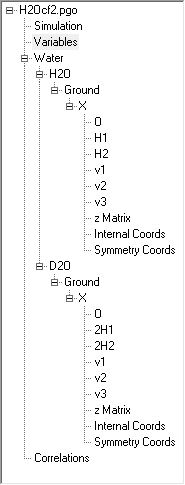
Worked Example - Setting up a combined force field analysis for H2O and D2O

In this example the basic file set up for the force field of H2O is extended to allow data from D2O to be included. This demonstrates how to combine multiple isotopologues in one file, and use the same force constants and geometry for each. The D2O experimental data is taken from the same source as the H2O data.

Converting to global variables

The first step is to move the variables describing the geometry and force constants to a global Variables object. We start with H2Osf4.pgo from the simple force field analysis.
  1. Create the variables object by right clicking on the topmost object in the constants window (the file name) and selecting "Add New ..., Variables".
  2. Click on the "Variables" object that has just been created, and set "Global" to True. This makes the parameters created in the variables object easier to use, as the names can be used without qualification.
  3. Create the variables required - for H2O we required rOH, HOH, kstretch, kbend, kstrstr and kstrbend. Right click on Variables, select "Add Parameter..." and enter the list of names as above.
  4. The variables will all be created with zero initial values. Copy and paste the values found previously from the "z Matrix" and "Internal Coords" objects. (This can be done with a few mouse clicks: click and drag in the source object to select the values, right click and select copy, click in the first cell in the destination Variables object and right click and select paste.)
  5. The original variables are now redundant, and must be deleted. Click on "z Matrix", right click on any of the parameters and select "Remove All Parameters". Repeat the process for "Internal Coords".
If everything has been done correctly, all the previous calculations should still work - try clicking on "Operate" and select "Check" in one of the windows. The file is available as H2Ocf1.pgo.

Setting up the calculation for D2O

To set up the calculation for D2O as well as H2O the simplest way is to duplicate the H2O objects, and modify then as required:
  1. To make things clearer some renaming will help. Right click on "Species", select "Rename" and enter "Water". All the isotopologues will be under this.
  2. Right click on "VibratingMolecule", select "Rename" and enter "H2O". This node, and everything under it, is specific to H2O.
  3. Duplicate the "H2O" object by right clicking on it, and selecting copy. The right click on "Water" and select paste.
  4. Rename the new object: right click on "Copy of H2O", select "Rename" and enter "D2O".
  5. The D2O object now needs adjusting; in this case the only thing that needs changing are the nuclear masses. Right click on the "z Matrix" object under "D2O" and select "View".
  6. The isotope can be specified as a leading number for the atom name in the first column. To specify deuterium, change "H1" and "H2" in the first column to "2H1" and "2H2".
This completes the set up for D2O. The file is available as H2Ocf2.pgo, which has the following structure:

We can now calculate the rotational constants and vibrational frequencies for D2O; right click on "X" under "D2O" and select "Print Information". Key values include:
Rotational Constants / cm-1 1..3
    15.49461654     7.21393246     4.92224832

L Matrix
/cm-1      2646.0063      1162.6458      2752.8384
L       v1             v2             v3             
  S1    0.7363239075   0.0191938829   0.0000000000
  S2   -0.1498032118   1.1095331612   0.0000000000
  S3    0.0000000000   0.0000000000   0.7586150835

Fitting to H2O and D2O

The results above are reasonable, but we can refine the geometry and force constants to give a better combined fit. We need to put the observations in a separate file as before, with a little extra information to specify the isotopologue. The values for H2O need to look like this:

Parameter H2O X Bx = 27.8778
Parameter H2O X By = 14.5092
Parameter H2O X Bz = 9.2869

Parameter H2O.X.v1.Omega = 3656.65
Parameter H2O.X.v2.Omega = 1594.59
Parameter H2O.X.v3.Omega = 3755.79
(Note that the modes have been renumbered to take account of the introduction of symmetry coordinates.) Adding the D2O values is straightforward:
Parameter D2O.X.Bx = 15.3846
Parameter D2O.X.By =  7.2716
Parameter D2O.X.Bz =  4.8458

Parameter D2O.X.v1.Omega = 2671.80
Parameter D2O.X.v2.Omega = 1178.33
Parameter D2O.X.v3.Omega = 2788.05

This is available in H2Ocf1.obs. Fitting can now proceed as before:

  1. Open the log window ("View, Log...") if it is not open already.
  2. The text box at the top needs to contain the file name; drag and drop the file onto the window, or use the browse button to the right of the text box to bring up a file browsing dialog.
  3. Make sure the fit type at the top left is set to "Line".
  4. Given the significant change made to the observations file, it is probably best to do a fit cycle with no parameters floated to check that the file has been set up correctly. To fix all the parameters click on "Fix All" in the constants window. Pressing the "Fit" button will give 
    Residuals before fit
        J'S' #'    J"S" #"     Observed    Calculated      Obs-Calc StdDev 
    H2O X.Bx                    27.8778       27.8531        0.0247 1        :   4:H2Ocf1.obs
    H2O X.By                    14.5092       14.4168        0.0924 1        :   5:H2Ocf1.obs
    H2O X.Bz                     9.2869        9.4997       -0.2128 1        :   6:H2Ocf1.obs
    H2O v1.Omega              3656.6500     3656.6500       -0.0000 1        :   8:H2Ocf1.obs
    H2O v2.Omega              1594.5900     1594.5900       -0.0000 1        :   9:H2Ocf1.obs
    H2O v3.Omega              3755.7900     3755.7900       -0.0000 1        :  10:H2Ocf1.obs
    D2O X.Bx                    15.3846       15.4946       -0.1100 1        :  12:H2Ocf1.obs
    D2O X.By                     7.2716        7.2139        0.0577 1        :  13:H2Ocf1.obs
    D2O X.Bz                     4.8458        4.9222       -0.0764 1        :  14:H2Ocf1.obs
    D2O v1.Omega              2671.8000     2646.0063       25.7937 1        :  16:H2Ocf1.obs
    D2O v2.Omega              1178.3300     1162.6458       15.6842 1        :  17:H2Ocf1.obs
    D2O v3.Omega              2788.0500     2752.8384       35.2116 1        :  18:H2Ocf1.obs

    12 Observations,  0 Parameters
    Average Error: 13.3891789207862
    suggesting the file is correct.
  5. The obvious first step is to try floating the two geometrical parameters (rOH and HOH) and the diagonal force constants kstretch and kbend. To do this, click on "Variables" in the constants window and change the "no" by each of the parameters to "yes" by clicking on the "no".
  6. Pressing the "Fit" button will now carry out one cycle of least squares fitting. As before a few cycles are required for convergence, which gives:
    Residuals before fit
        J'S' #'    J"S" #"     Observed    Calculated      Obs-Calc StdDev 
    H2O X.Bx                    27.8778       28.1371       -0.2593 1        :   4:H2Ocf1.obs
    H2O X.By                    14.5092       13.8615        0.6477 1        :   5:H2Ocf1.obs
    H2O X.Bz                     9.2869        9.2866        0.0003 1        :   6:H2Ocf1.obs
    H2O v1.Omega              3656.6500     3668.6222      -11.9722 1        :   8:H2Ocf1.obs
    H2O v2.Omega              1594.5900     1601.7479       -7.1579 1        :   9:H2Ocf1.obs
    H2O v3.Omega              3755.7900     3772.8698      -17.0798 1        :  10:H2Ocf1.obs
    D2O X.Bx                    15.3846       15.6526       -0.2680 1        :  12:H2Ocf1.obs
    D2O X.By                     7.2716        6.9361        0.3355 1        :  13:H2Ocf1.obs
    D2O X.Bz                     4.8458        4.8063        0.0395 1        :  14:H2Ocf1.obs
    D2O v1.Omega              2671.8000     2652.9815       18.8185 1        :  16:H2Ocf1.obs
    D2O v2.Omega              1178.3300     1168.6079        9.7221 1        :  17:H2Ocf1.obs
    D2O v3.Omega              2788.0500     2766.9424       21.1076 1        :  18:H2Ocf1.obs

    12 Observations,  4 Parameters
    Initial Average Error: 13.1393954167445
    Predicted New Error:   13.1393954167445
    Parameters:
      # Old                 New                 Std Dev   Change/Std Sens    Summary              Name
      1 .968526948276958    .968526956897577    .17225937    0.0000  .000557 0.969(172)           Variables rOH
      2 106.642664066447    106.642663838532    2.9141525    0.0000  .240594 106.6(29)            Variables HOH
      3 7.73033457831899    7.73033457816424    .03123699    0.0000  .002705 7.730(31)            Variables kstretch
      4 .663596548317366    .663596560444018    .23589257    0.0000  .000763 0.664(236)           Variables kbend

    Correlation Matrix
           1       2       3       4
      1   1.000
      2   0.124   1.000
      3   0.000   0.004   1.000
      4   0.999   0.114   0.000   1.000
  7. An important check is that the assignment has not changed - check using the l matrix window that the vibrational assignment is correct for both H2O and D2O.
  8. It is also possible to float the kstrstr parameter as in the simple fit. While the fit is stable, the kstrstr parameter is not determined - the fitted value is -0.053(97) and the fit is not significantly improved. This suggests at the level of accuracy possible with this harmonic model it might be better to fix this at zero.