Molecule Types Linear Molecules <Prev Next>

Worked Example - The Schumann-Runge Bands of O2

The key parameters required for a simulation of a linear molecule spectrum are summarized in Making a Linear Molecule Data File. The steps below show how to do this for part of the Schumann-Runge Bands of O2, which are responsible for atmospheric absorption around 190nm.

The Constants

The molecular parameters are required for any simulation; an excellent compilation of constants for diatomic molecules can be found in the NIST Chemistry web book at  http://webbook.nist.gov/chemistry/. This database includes an electronic version of information in the book K.P. Huber and G. Herzberg, "Constants of Diatomic Molecules". A formula search on O2 with "Constants of diatomic molecules" selected yields many states; the Schumann-Runge Bands arise from the  B3Σu- - X3Σg-. (The ν00 value can be a helpful guide here as to which band to use.) An abbreviated version of the table is presented below, with just the B and X state entries.
State Te ωe ωexe ωeye Be αe γe De βe re Trans. ν00
B 3Σu- 49793.28 709.31 a Z 10.65 a -0.139 0.81902 a b 0.01206 a -5.56E-4 4.55E-6 c   1.60426 B ↔ X R 49358.15 Z
X 3Σg- 0 1580.193 Z 11.981 d .04747 [1.4376766] e 0.01593 f   [4.839E-6] e   1.20752    
The footnotes contain the source of the information, and also some additional constants that are often essential to obtaining a reasonable simulation including the the spin orbit coupling constant, A (required if the electron spin and orbital angular momentum are both non zero) and and the spin-spin coupling constant, λ (required if the electron spin is >= 1; LambdaSS in PGOPHER). The more important ones are referenced in the in the table above:
a) ωeye = -0.139, γe = -0.000556 from a low order fit to v ≤ 4.
b) The spin splitting constants at low v are λ = 1.5, -γ ~ 0.04 cm-1.
c) β =0.22E-6 for low v.
d) ωeze = -0.001273
e) Spin splitting constants λ0 = +1.9847511, γ0 = -0.00842536;
f) B1 = 1.42192

Vibrational Dependence of The Constants

Much of this information is concerned with the variation of constants with vibrational number, v. The numbers in the main table are not suitable for direct entry into PGOPHER, as they are equilibrium values. For each vibronic transition, with a particular v' and v" a separate set of constants is required. To choose a specific case we will simulate the B3Σu- v' = 2 - X3Σg- v" = 0 transition.

The band origin

The first step is to calculate the band origin. For this purpose the following expression must be evaluated for each vibrational state:
E(v) = Te + ωe(v + ½) − ωexe(v + ½)2 + ωeye (v + ½)3 + ωeze (ν + ½)4
For B3Σu- v' = 2 this gives:
Origin = 49793.28 +  709.31(2 + ½) − 10.65(2 + ½)2 + -0.139 (2 + ½)3 =  51497.82 cm-1.
Note that ωeze is not given, though footnotes not reproduced here indicate more information is available; G(v) values or band origins are normally the values tabulated in the primary literature.
For X3Σg- v" = 0 this gives :
Origin = 1580.193(0 + ½) −  11.981(v + ½)2 + 0.04747(0 + ½)3 + -0.001273(0 + ½)4 = 787.11 cm-1. Here ωeze is given.
The band origin for the transition is then 51497.82 - 787.11 = 50710.71 cm-1. Note that either the two separate origins can be entered, or the ground state origin can be left at zero and the difference entered for the excited state origin

The Rotational Constant

A similar process is required for the rotational constant; the equation is similar:
Bv = Be − αe(v + ½) + γe(v + ½)2 + ...
For B3Σu- v' = 2 this gives:
B2 =  0.81902 −  0.01206(v + ½) +  -5.56E-4(v + ½)2 = 0.785395 cm-1.
For X3Σg- v" = 0 the [] indicates that the value is for v = 0 so no evaluation is necessary; a value for v = 1 is given in the footnote and references to sources for higher v are given in the full table.
The centrifugal distortion constants follow a similar equation:
Dv = De − βe(v + ½) + ...
though this can be omitted for a rough simulation.

Other Constants

The spin-orbit (A) and spin-spin (λ) constants are also often crucial to obtaining a reasonable simulation; in this case the spin-orbit constants are zero as both states are Σ, but the spin-spin constants are required as S = 1. Both are only given in the footnotes:
For B3Σu- v' = 2, λ = 1.5
For X3Σg- v" = 0, λ = +1.9847511
The spin-rotation constant, γ, is also given for these two states, though this is normally less important.

Setting up the simulation

There is now enough information to produce a basic simulation in PGOPHER:
  1. Click on File, New, Linear Molecule
  2. Select View, Constants
  3. Click on LinearMolecule. This sets the parameters common to all states, and the ones that need to be changed from the default values are:
    1. Symmetric = "True" (as the molecule has a centre of symmetry)
    2. AsymWt = 0 (This is the statistical weight of antisymmetric states, and the zero reflects the fact that half the levels of O2 are missing.
  4. Click on "v=0" and enter the information for X3Σg- v = 0
    1. Lambda = Sigma-
    2. S = 1 (the electron spin)
    3. gerade = True (the default, indicating g symmetry)
    4. B = 1.4376766
    5. LambdaSS (λ) = 1.9847511
  5. Click on "v=1" and enter the information for B3Σu- v = 2
    1. Lambda = Sigma-
    2. S = 1 (the electron spin)
    3. gerade = False (to indicate u symmetry)
    4. Origin = 50710.71
    5. B = 0.785395
    6. LambdaSS (λ) = 1.5
    7. To avoid confusion the "v=1" name should be changed; right click on "v=1" and select rename to do this. The name does not affect the calculation, but "v=2" would be the logical choice!
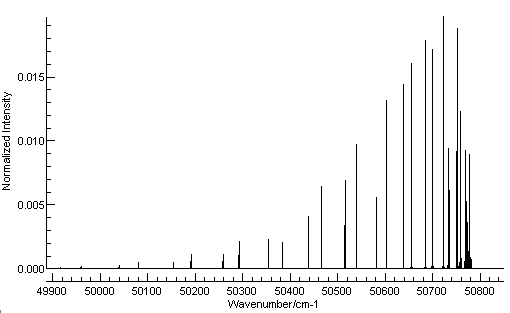
This should be enough to for a basic simulation; press the simulate button (Simulate) and then the all button (all) and you should see a simulation. With a small adjustment of the plot range it should look like this:
Basic O2 B-X 2-0 simulation

Checking and refining the simulation

    It is important to check the simulation, not only because it is easy to make mistakes in the steps above, but also because there can be differences in the definitions of the constants used. Checking against tabulated line positions or published spectra is an effective check; note the facility for overlaying pictures (from a Journal for example) onto a simulation.
    In this case a numerical spectra is available from the Harvard-Smithsonian Center for Astrophysics website (http://cfa-www.harvard.edu/), specifically the CfA Molecular Data. For oxygen, measured cross sections are available; follow the links Measured cross sections: Schumann-Runge bands of all isotopes, 179 nm - 203 nm,  (2,0) band, 50050-50720 cm-1 . This gives a table of numbers which can be directly copied into PGOPHER; in your browser use "select all", "copy" and then in PGOPHER use "Overlays, Paste". The observed spectrum will appear above the simulation.
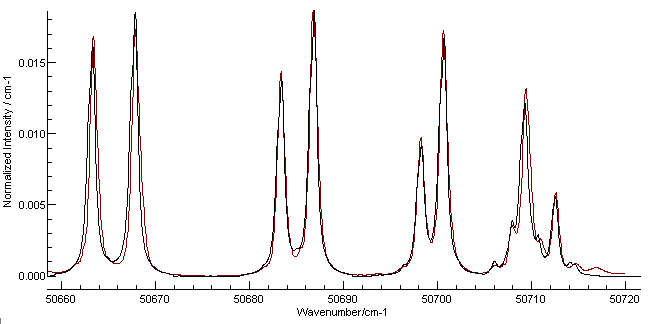
    Following the instructions above gives a spectrum a reasonable simulation, and a good visual match can be obtained with a Lorentzian linewidth of 0.65 cm-1 (The "Lor" box on the main window toolbar). The width does not take effect in the simulation if the display is too compressed; zooming in to the portion around the band origin gives the following plot:
Region around band origin
Here the red line is the Harvard data and the black is the simulation. The most obvious discrepancy is on the right, and is most likely a transition from another band. The line positions are not absolutely perfect, but this could be improved by adding D and γ to the simulation and checking the literature for more accurate constants. The overall experimental spectrum also shows additional lines at the other end, probably from the (4-1) band. (An obvious exercise for the reader is to check this using by following the procedure above for this band.)