| |
<Prev Next> |
The key parameters required for a simulation of a vibrational spectrum are summarized in Making a basic data file for simulating vibrational structure. The steps below show how to do this for the first band in the photoelectron spectrum of water, using literature values for constants where available. See the related worked example, Predicting the Photoelectron Spectrum of H2O using ab inito Calculations for an alternative approach.
An excellent compilation of spectroscopy constants for can be found in the NIST Chemistry web book at http://webbook.nist.gov/chemistry/. A formula search on H2O with ions not excluded yields information on several isotopes; selecting the main isotope and then "Vibrational and/or electronic energy levels" yields for H2O:
| Sym Species |
No | Approximate type of mode |
Selected Freq |
| a1 |
1 |
Sym str |
3657 |
| a1 |
2 |
Bend |
1595 |
| b1 |
3 |
Anti str |
3756 |
Confusingly the asymmetric stretch, v3, is shown as
having b1 symmetry in this table, though the modern
convention is to classify this mode as b2. The b2
symmetry follows if the out of plane axis is chosen to be the x axis, the current
convention, while b1 symmetry follows if the out of
plane axis is chosen to be the y axis. The choice is not
necessarily important for the simulation, but it is important to
be consistent.
Selecting "Gas phase ion energetics data" gives an ionization
potential of 12.621 eV; see below for some discussion of this
value.
For the ion information on several states is available; taking
just the most recent ground state (X state) gas phase values:
| Vib Sym |
No | Approximate type of mode |
cm-1 |
| a1 |
1 |
Sym stretch |
3197.97 |
| a1 |
2 |
Bend |
1408.42 |
| b2 |
3 |
Asym Stretch |
3253.91 |
Note that the asymmetric stretch is shown as b2
here. More detailed simulations would have to consider
anharmonicities.
This should be enough for a basic simulation; press the
simulate button ( ) and then the all
button (
) and then the all
button ( ) and you should see a simulation,
though it will essentially have only one peak as we are assuming
no geometry change on ionization.
) and you should see a simulation,
though it will essentially have only one peak as we are assuming
no geometry change on ionization.
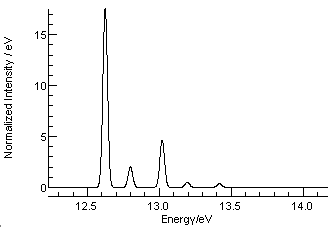
It is important to check simulations, not only because it is easy to make mistakes in the steps above, but also because there can be differences in the definitions of the constants or other factors, such as the different choice of symmetry for the asymmetric stretch described above. Checking against tabulated line positions or published spectra is an effective check; note the facility for overlaying pictures (from a Journal for example) onto a simulation.
In this case an experimental simulation is
available from R. N. Dixon, G. Duxbury, J. W. Rabalais and L.
Åsbrink, "Ro-vibronic structure in the photoelectron
spectra of H2O, D2O and HDO", Molecular
Physics, 31, 423, http://dx.doi.org/10.1080/00268977600100311.
This shows that, while the first peak is indeed the strongest,
about ¼ of the intensity is in the other peaks. Manually
adjusting the vibrational displacements to v1 = 0.07, v2 = 0.07
gives a reasonable match for the observed intensities. As a
final point, the peaks are all shifted from the simulation - the
strongest peak is simulated at 12.550 eV but measured at 12.624
eV. The difference here (0.074) is likely to be the zero point
energy; this could be checked by looking at the individual
vibrational levels - selecting "View", "States". Adding 0.074eV = 600 cm-1
to the ion origin brings the spectra into line, as shown in the
plot below.