| |
<Prev Next> |
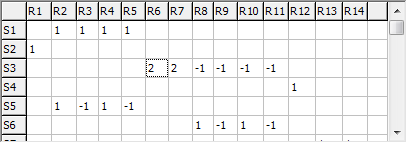
Symmetry coordinates, S, are specified by giving the
transformation matrix, U, between S and the
internal coordinates, R:
S = U R = U B Δx
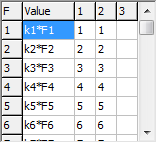
The symmetry coordinates window, shown below for
C2H4, allows the display and editing of the
U matrix and (optionally) the force field in terms of
symmetry coordinates, F. To create a symmetry coordinates
object, right click on the Electronic
State object object and select "Add New...,
Symmetry Coords". To bring up the window right click on the
symmetry coordinates object and select "View...". If a symmetry
coordinates object is not present, or the U matrix is left
blank, an identity matrix is assumed for the U matrix.
Note that the current version of the program ignores the point
group set for the molecule as a whole, and the symmetry set for
the individual vibrational modes when doing the force field
calculation. This may be changed in future versions of the
program.
With the current version the choice of symmetry co-ordinates for degenerate modes may require some care; the values calculated for the Coriolis coupling constants and some other vibration-rotation constants can be sensitive to the choice made. This is partly mitigated by forcing the largest coefficient for each mode in the L matrix to be positive by multiplying the vibrational mode by -1 as required. The PreserveS flag (see below) can also be helpful in keeping modes consistent. The simplest results are obtained if the co-ordinates chosen for different degenerate modes have the same transformation properties under the operations of the point group.
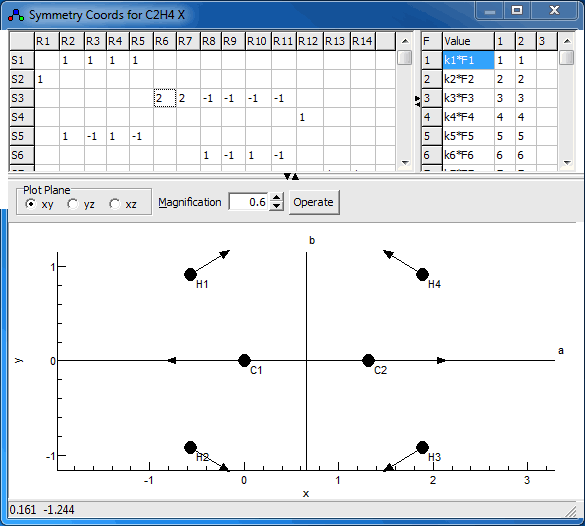
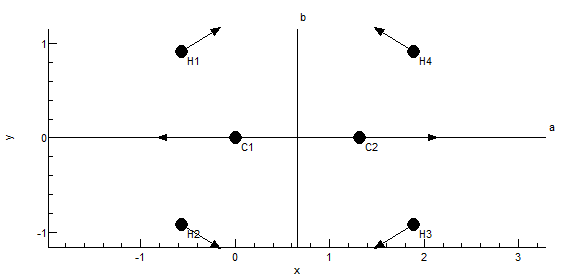
The plot at the bottom shows the current symmetry coordinate, i.e. the selected row in the top left grid. The arrows indicate how far each atom moves. The plot updates semi-automatically; use "Operate, Check" to force an update.
| Check |
Check the contents of the top grids, and
update the plot to match |
| Apply |
Check the contents of the top grids, and
display the details of the vibrational mode calculation in
the Log Window. This also forces
other objects to update. |
| Make Extra Operators | Create vibrational perturbations - see Other Potential Terms. |
| Show F Matrix | Print the F matrix in the Log
Window calculated from the l matrix
elements and frequencies given in the vibrational mode objects.
The transformation is done by calculating the matrix L,
which relates the symmetry coordinates, S, and
normal coordinates, Q:S = L QThe L matrix is available from: L = U B M-½ lproviding the internal coordinates are fully specified and the F matrix can then be calculated from: F = (L-1)T λ L-1Note that the U matrix is not necessarily required, but if there are redundant internal coordinates L-1 can't be calculated. In this case an alternative relationship can be used: F = L λ LTprovided that L LT= 1. |
| Set F Matrix | Clear the f matrix grid (top right) and set it from the l matrix elements and frequencies given in the vibrational mode objects. See the entry above for details of the calculation. |
| Sort F Matrix by Value | Sort the F matrix grid (top right) in descending order of the first column. |
| Sort F Matrix by Mode | Sort the F matrix grid (top right) by mode numbers, with diagonal elements first. |
V = ½ ST F S = ½ Σij FijSiSj